GloVe

概述

模型目标：进行此的向量化表示，使得向量之间尽可能多地蕴含语义和语法的信息。
输入：语料库
输出：词向量
方法概述：首先基于语料库构建词的共现矩阵，然后基于共现矩阵和GloVe模型学习词向量。

开始->统计共现矩阵->训练词向量->结束

统计共现矩阵

设共现矩阵为X，其元素为$X_{i,j}$。
$X_{i,j}$的意义为：在整个语料库中，单词i和单词j共同出现在一个窗口中的次数。
举个栗子：
设有预料库：

i love you but you love him i am sad

这个小小的预料库只有一个句子，涉及到7个单词：i、love、you、but、him、am、sad。
如果我们采用一个窗口为5（左右长度都为2）的统计窗口，使用窗口将整个语料库遍历一遍，即可得到共现矩阵X，自己想象！

使用GloVe模型训练词向量

模型公式

先看模型，代价函数长这个样子：

$J = \sum_{i,j}^{N}{f(X_{i,j})(v_{i}^{T}v_{j}+b_i + b_j - log(X_{i,j}))^{2}}$

$v_{i},v_{j}$是单词i和单词j的词向量，$b_{i},b_{j}$是两个标量（作者定义的偏差项），f是权重函数（具体函数公式及功能下一节介绍），N是词汇表的大小（共现矩阵维度为N*N）。
可以看到，GloVe模型没有使用神经网络的方法。

模型怎么来的

那么作者为什么这么构造模型呢？首先定义几个符号：

$X_{i} = \sum_{j=1}^{N}{X_{i,j}}$

其实就是矩阵单词i那一行的和；

$P_{i,k}= \frac{X_{i,k}}{X_{i}}$

条件概率，表示单词k出现在单词i语境中的概率；

$ratio_{i,j,k} = \frac{P_{i,k}}{P_{j,k}}$

两个条件概率的比率。
作者的灵感是这样的：
作者发现，$ratio_{i,j,k}$这个指标是有规律的，规律统计在下表：

我们可以使用它观察出两个单词i和j相对于单词k哪个更相关（relevant）。这个是很直观的。因此，以上推断可以说明通过概率的比例而不是概率本身去学习词向量可能是一个更恰当的方法.
思想：假设我们已经得到了词向量，如果我们用词向量$v_{i},v_{j},v_{k}$ 通过某种函数计算$ratio_{i,j,k}$，能够同样得到这样的规律的话，就意味着我们词向量与共现矩阵具有很好的一致性，也就说明我们的词向量中蕴含了共现矩阵中所蕴含的信息。
设用词向量$v_{i},v_{j},v_{k}$计算$ratio_{i,j,k}$的函数为$g(v_{i},v_{j},v_{k})$(我们先不去管具体的函数形式)，那么应该由：

$\frac{P_{i,k}}{P_{j,k}} = ratio_{i,j,k}= g(v_{i},v_{j},v_{k})$

即：

$\frac{P_{i,k}}{P_{j,k}} = g(v_{i},v_{j},v_{k})$

即二者应该尽可能地接近；
很容易想到用二者的差方来作为代价函数：

$J = \sum_{i,j,k}^{N}{(\frac{P_{i,k}}{P_{j,k}}-g(v_{i},v_{j},v_{k}))^{2}}$

但是仔细一看，模型中包含3个单词，这就意味着要在NNN的复杂度上进行计算，太复杂了，最好能再简单点。
现在我们来仔细思考$g(v_{i},v_{j},v_{k})$，或许它能帮上忙；
作者的脑洞是这样的：
1.要考虑单词i和单词j之间的关系，那$g(v_{i},v_{j},v_{k})$中大概有这么一项吧：$v_{i}-v_{j}$;嗯，合理，在线性空间中考察两个向量的相似性，不失线性地考察，那么$v_{i}-v_{j}$大概是个合理的选择；
2.$ratio_{i,j,k}$是个标量，那么$g(v_{i},v_{j},v_{k})$最后应该是个标量啊，虽然其输入都是向量，那内积应该是合理的选择，于是应该由这么一项吧：$(v_{i}-v_{j})^{T}v_{k}$。
3.然后作者又往$(v_{i}-v_{j})^{T}v_{k}$的外面套了一层指数运算exp(),得到最终的$g(v_{i},v_{j},v_{k})=exp((v_{i}-v_{j})^{T}v_{k})$；
最关键的第3步，为什么套了一层exp()？
套上了之后，我们的目标是让一下公式尽可能地成立：

$\frac{P_{i,k}}{P_{j,k}} = g(v_{i},v_{j},v_{k})$

即：

$\frac{P_{i,k}}{P_{j,k}} = exp((v_{i}-v_{j})^{T}v_{k})$

即：

$\frac{P_{i,k}}{P_{j,k}} = exp(v_{i}^{T}v_{k}-v_{j}^{T}v_{k})$

即：

$\frac{P_{i,k}}{P_{j,k}} = \frac{exp(v_{i}^{T}v_{k})}{exp(v_{j}^{T}v_{k})}$

然后就发现找到简化方法了：只需要让上式分子对应相等，分母对应相等，即：$P_{i,k} = exp(v_{i}^{T}v_{k})$并且$P_{j,k} = exp(v_{j}^{T}v_{k})$。
然而分子分母形式相同，就可以把两者统一考虑了，即：

$P_{i,j} = exp(v_{i}^{T}v_{j})$

本来我们追求：

$\frac{P_{i,k}}{P_{j,k}} = g(v_{i},v_{j},v_{k})$

现在只需要追求：

$P_{i,j} = exp(v_{i}^{T}v_{j})$

两边去个对数：

$log(P_{i,j}) = v_{i}^{T}v_{j}$

那么代价函数就可以简化为：

$J = \sum_{i,j}^{N}{(log(P_{i,j})-v_{i}^{T}v_{j})^2 }$

现在只需要在NN的复杂度上进行计算，现在关于为什么第3步中，外面套一层exp()就清楚了，正是因为套了一层exp()，才使得差形式变成商形式，进而等式两边分子分母对应相等，进而简化模型。
然而，出了点问题。仔细看这两个句子：
$log(P_{i,j}) = v_{i}^{T}v_{j}$和$log(P_{j,i}) = v_{j}^{T}v_{i}$。
$log(P_{i,j})$不等于$log(P_{j,i})$但是$v_{i}^{T}v_{j}$等于$v_{j}^{T}v_{i}$；即等式左侧布局有对称性，但是右侧具有对称性。数学上出了问题。
补救一下就好了。现在讲代价函数中的条件概率展开：

$log(P_{i,j}) = v_{i}^{T}v_{j}$

即为：

$log(X_{i,j}) - log(X_{i}) = v_{i}^{T}v_{j}$

此时，我们发现因为等号右侧的log(Xi)
的存在而且这个也是不满足对称性的。而其实是log(Xi)跟j独立的，它只跟i有关，于是我们可以针对$v_{i}$增加一个bias term bi把它替换掉，为了对称，那就一不做二不休，再针对$v_{j}$增加一个bias term bj于是我们有：

$log(X_{i,j}) = v_{i}^{T}v_{j} + b_{i} + b_{j}$

于是代价函数就变成了：

$J = \sum_{i,j}^{N}{(v_{i}^{T}v_{j} + b_{i} + b_{j} - log(X_{i,j}))^{2}}$

然后基于出现频率越高的词对儿权重应该越大的原则，在代价函数中添加权重项，于是代价函数进一步完善：

$J = \sum_{i,j}^{N}{f(X_{i,j})(v_{i}^{T}v_{j} + b_{i} + b_{j} - log(X_{i,j}))^{2}}$

具体权重函数应该是怎么样的呢？
首先应该是非减的，其次当词频过高时，权重不应过分增大，作者通过实验确定权重函数为：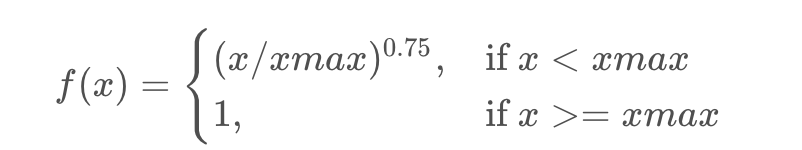

GloVe的训练过程是怎样的？

1.实质上还是监督学习：虽然glove不需要人工标注为无监督学习，但实质还是有label就是 $log(X_{ij})$ 。
2.向量 w 和 $\tilde{w}$为学习参数，本质上与监督学习的训练方法一样，采用了AdaGrad的梯度下降算法，对矩阵 X 中的所有非零元素进行随机采样，学习曲率（learning rate）设为0.05，在vector size小于300的情况下迭代了50次，其他大小的vectors上迭代了100次，直至收敛。
.3最终学习得到的是两个词向量是 $\tilde{w}$ 和 w ，因为 X 是对称的（symmetric），所以从原理上讲$\tilde{w}$ 和 w ，是也是对称的，他们唯一的区别是初始化的值不一样，而导致最终的值不一样。所以这两者其实是等价的，都可以当成最终的结果来使用。但是为了提高鲁棒性，我们最终会选择两者之和 $w+\tilde{w}$ 作为最终的vector（两者的初始化不同相当于加了不同的随机噪声，所以能提高鲁棒性）。

到此，整个模型就介绍完了。
以上内容其实不能完全称之为推导，因为有很多不严谨的地方，只能说是解释作者如何一步一步构造出这个公式的，仅此而已。