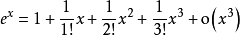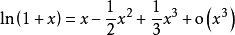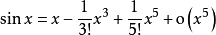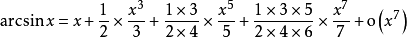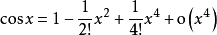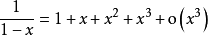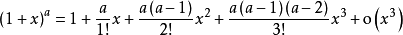函数的泰勒(Taylor)展开式

泰勒公式是将一个在$x=x_{0}$处具有n阶导数的函数f(x)利用关于$(x-x_{0})$的n次多项式来逼近函数的方法。
若函数f(x)在包含$x_{0}$的某个闭区间[a,b]上具有n阶导数，且在开区间(a,b)上具有(n+1)阶导数，则对闭区间[a,b]上任意一点x，成立下式：

$$f(x) = \frac{f(x_{0})}{0!}+\frac{f'(x_{0})}{1!}(x-x_{0})+\frac{f''(x_{0})}{2!}(x-x_{0})^{2}+...+\frac{f^{(n)}(x_{0})}{n!}(x-x_{0})^{n}+R_{n}(x)$$

其中，$f^{(n)}(x)$表示f(x)的n阶导数，等号后的多项式称函数f(x)在$x_{0}$处的泰勒展开式，剩余的$R_{n}(x)$是泰勒公式的余项，是$(x-x_{0})n$的高阶无穷小。
余项
泰勒公式的余项$R_{n}(x)$可以写成以下几种不同的形式:
1、佩亚诺(Peano）余项：

$$R_{n}(x)=o[(x-x_{0})^{0}]$$

这里只需要n阶导数存在
2、施勒米尔希-罗什(Schlomilch-Roche）余项：

$$R_{n}(x)=f^{n+1}[x_{0}+\theta(x-x_{0})]\frac{(1-\theta)^{n+1-p}(x-x_{0})^{n+1}}{n!p}$$

其中$\theta\in(0,1)$,p为任意正实数。（注意到p=n+1与p=1分别对应拉格朗日余项和柯西余项）
3、拉格朗日（Lagrange）余项：

$$R_{n}(x)=f^{n+1}[x_{0}+\theta(x-x_{0})]\frac{(x-x_{0})^{n+1}}{(n+1)!}$$

其中$\theta\in(0,1)$。
4、柯西（Cauchy）余项：

$$R_{n}(x)=f^{n+1}[x_{0}+\theta(x-x_{0})]\frac{(1-\theta)^{n}(x-x_{0})^{n+1}}{n!}$$

其中$\theta\in(0,1)$。
5、积分余项：

$$R_{n}(x)=\frac{(-1)^{n}}{n!}\int_{a}^{x}{(t-x)f^{(n+1)}(t)dt}$$

其中以上诸多余项事实上很多是等价的。

在带佩亚诺余项的情况下列举一些常用函数的泰勒公式：