Ensemble的主要思路大概可理解为‘群殴’的意思。假设你有一堆的模型,他们是各种各样的,这时,集合起来让他们各司其职,能达到更好啊效果。
Bagging
回顾一下模型误差的由来。模型误差的主要原因可解析为偏差(Bias)和方差(Variance)。方差形容的是模型输出值与真实值之间的误差,方差形容的是模型输出值与模型输出值的期望之间的误差,可理解为模型的稳定性。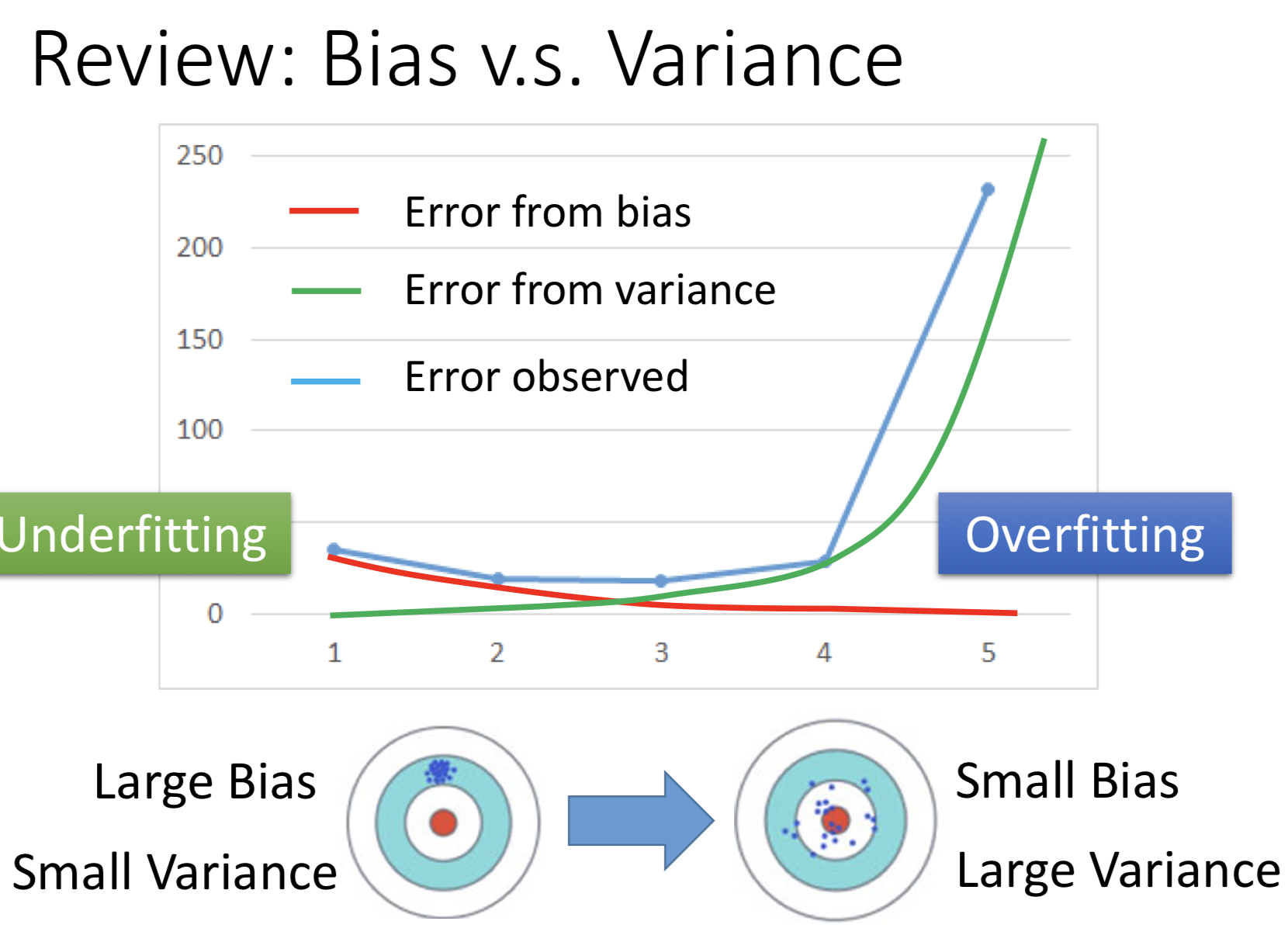
横坐标代表模型的复杂度,模型比较简单时,方差小,偏差大(这时模型的能力不足,偏差大;输出出错且稳定,所以方差小);模型很复杂时,偏差小,方差大(这时模型能力过强,偏差已经降下来了,但由于出现过拟合问题,泛化能力就不强,就会出现不稳定的情况,方差大)。
看下面的例子
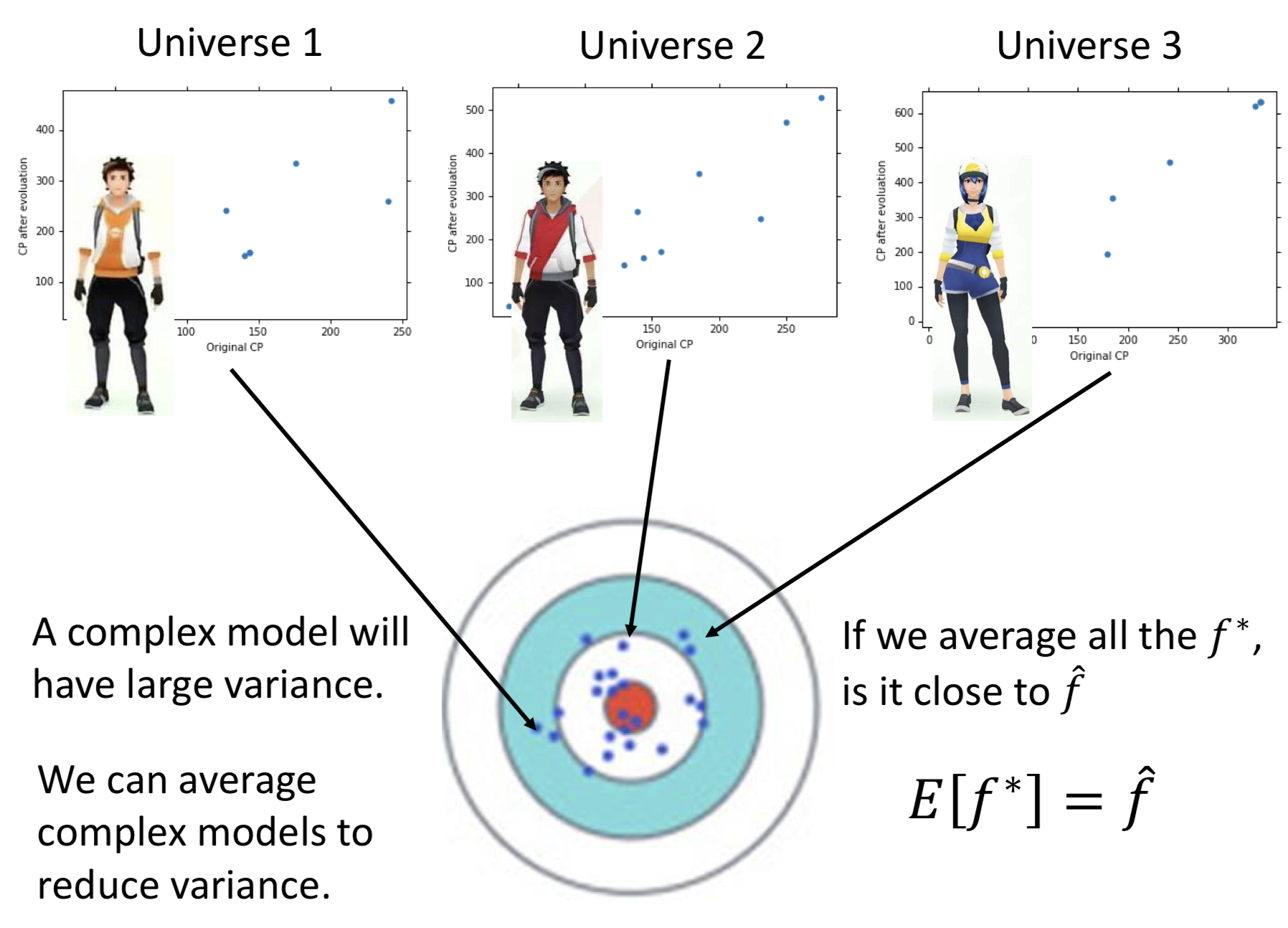
有三个平行宇宙,他们都要拟合图中宝可梦的cp值,但是他们的数据不太一样;这时假设他们都有一个非常复杂的模型$f^{}$,模型的bias小,variance大。而我们目标模型是$\hat{f}$,这时我们把$f^{}$平均起来,可以减小variance,更接近$\hat{f}$。这就是Bagging的思想。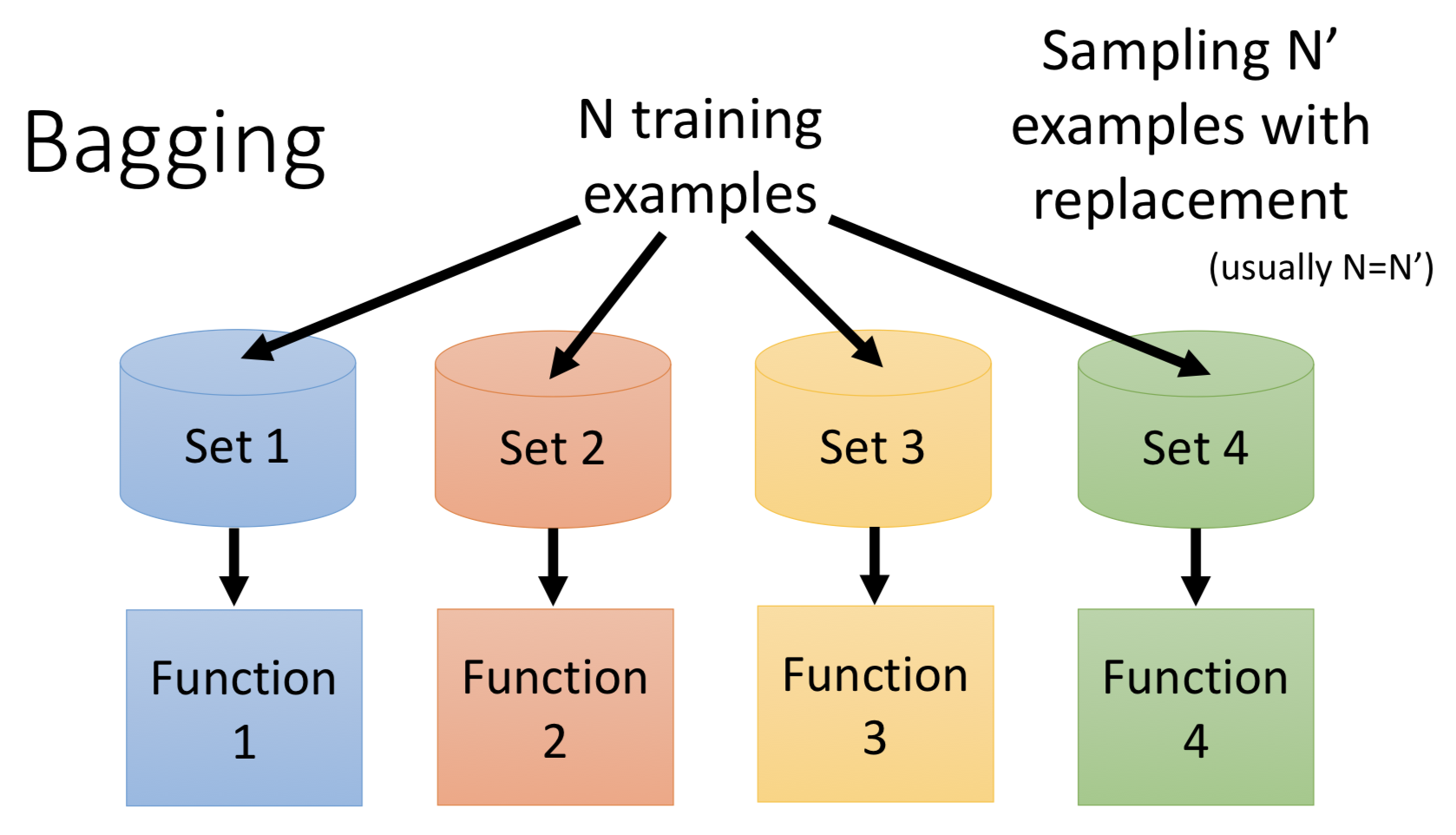
假设我们有N笔training data,我们有放回的从中sampling $N^{‘}$笔data(一般$N^{‘}$可以直接等于N,因为是有放回sample,得到的trainingset还是不一样的)。然后我们用着不同的多组trainingset去训练多个不同的model。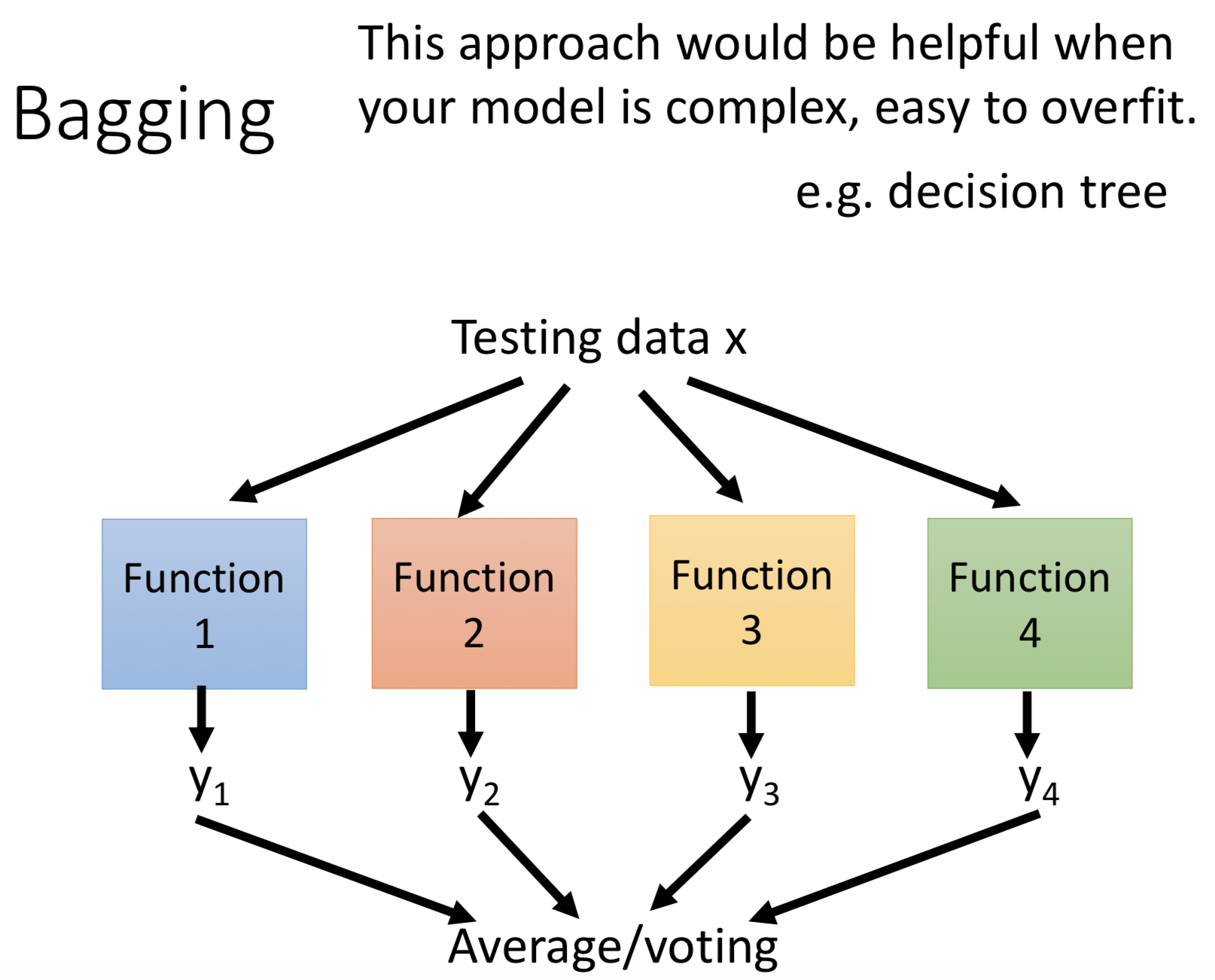
测试时,再把多个model的结果平均或者做投票(回归的做平均,分类问题做投票)得到你最终的结果(为什么Bagging会有效减少variance呢?你可以直接的理解为每个模型的拟合的数据不一样,过拟合的情况也不一样,最终的平均或投票,就是以多数非过拟合情况去平衡个别的过拟合情况,达到减小variance的效果)。
重点:当你的模型是复杂的且容易过拟合的时候,Bagging是非常有效的。(如决策树,当你的模型够深,模型是可以达到100%的正确率的,所以就非常适合,随机森林就是决策树的Bagging版本。问题来了,直觉上神经网络是很复杂的,按道理是容易出现过拟合的,但实操上你会发现neural newwork是很难做到100%的准确率的,问题往往是你很难再在training set上得到很好的结果。而且训练时间成本较高,做Bagging成本也会较高)
随机森林

随机深林可以说是决策树的Bagging版本。需要注意的是,随机森林仅仅重复sample训练集这个做法是不足够的,你的模型最终还是会很像,Bagging的效果会很一般。所以,还需要对数据集特征进行随机限制,如每棵树随机使用特征集中的一部分特征。
Out-ofbag(OOB) :随机森林有一个重要的优点就是,没有必要对它进行交叉验证或者用一个独立的测试集来获得误差的一个无偏估计。它可以在内部进行评估,也就是说在生成的过程中就可以对误差建立一个无偏估计。
实际上, 数据集D中的每一个样本都可以拿来做测试数据, 对于一个样本d, 森林中大约有1/e树是OOB的, 那么这1/e的树就构成了预测样本d的森林,用简单投票法计算分类结果. 从而得到总的error。
Boosting(Improving Weak Classifiers)
boosting做的事情是,假设我的model现在在训练集上的表现太弱了,boosting可以帮忙强化这些弱的model。(假设你的分类器只是比50%的正确率稍高这种弱智的模型,只要你使用boosting,可以得到0%的错误率,听起来真的很神奇)
Boosting的思路:假设你开始得到一个比较弱的算法f1,然后你要找一个f2,来帮助f1;要注意的两点是:
- f2不能和f1太像,如果两个太接近,那样效果就很差了
- f2要和f1是互补的
你得到f2之后,就可以继续在f2的基础上去找f3;如此得到一堆f,再把它们集合起来,就是一个超强的算法。
注意:Bagging所有模型是独立的,训练的时候是不相干的。而Boosting的模型是有序的,后面的模型都是根据前面的模型得来的,训练的时候是按顺序的。
下面是以二分类问题为例子

做Boosting,首先我们需要得到不同的分类器;
- 第一种方法是重复sample得到不同的training set从而得到不同的clasifier。(这种方法最终只会得到整数权重的sample)
- 第二种方法是给训练样本赋予不一样的权重,从而得到不一样的trainingset。而在实操上只要对loss函数做修改即可。如上图,在每一笔数据的error前面乘上每笔数据的权重u。这样的结果就像是这笔数据在你的数据集里出现了u次。
Adaboost

思路:假设你已经得到f1,你要找到新的trainingset,让f1在上面的表现是很差的,然后用来训练f2,这样得到的f2就是跟f1是互补的。
问题是怎么找到一个trainingset可以让f1坏掉呢?
做法就是调整训练数据的权重。
- 首先我们定义错误率$\epsilon$,下表对应第几个模型。Z是数据权重的和。假设我们现在训练好f1,$\epsilon_{1}<0.5$。
- 我们把训练好的f1的$u_{1}$换成$u_{2}$,这时使得error rate等于0.5(因为是二分类问题,0.5等同于随机猜测水平,就是坏掉了)。
- 然后我们在$u_{2}$(新的训练集)上去训练f2。
怎么去重新赋权数据(得到$u_{2}$呢?
思路就是增加f1中错误数据的权重,相对的同时减小正确数据的权重,达到一个错误率为0.5的情况;这时再去训练f2,$\epsilon$一定是比0.5小的。
具体来看,就是分类错误的,我们要把对应的权重乘以一个$d_{1},d_{1}>1$,分类对的除以$d_{1}$。
然后问题就变成怎么确定$d_{1}$?(下面的做法是强制对的和错的d相等,当然还有其他方法)

最后推算得到$d_{1}=\sqrt{\frac{(1-\epsilon_{1})}{\epsilon_{1}}}>1$
开始$u_{1}$是平均权重=1,循环T次,得到T个分类器。我们定义$\alpha_{t}=ln\sqrt{\frac{(1-\epsilon_{t})}{\epsilon_{t}}}$,简化表达式图,空白处为$-\hat{y}f_{t}(x^{n})$(预测正确为正,错误为负)。
最终我们得到T个分类器,然后我们可以简单的把它们加起来(因为是二分类问题),再根据正负值来判断类别。
还有另一种更好做法,把$\alpha_{t}$作为权重相乘,由上面推导可以得知,$\epsilon$越小,$\alpha$越大(直觉上错误率更低的分类器有更大的权重,是正确的)
下面看一个很简单的例子。
有几个正负的数据点,用decision stump(只砍一刀的decision tree)作为分类器。初始权重为$u_{1}=1$。T=1,假设第一刀砍玩后有三个错误点,计算得到$\epsilon_1,d_1,\alpha_1$,按照adaboost的方法,求得权重$u_{2}$。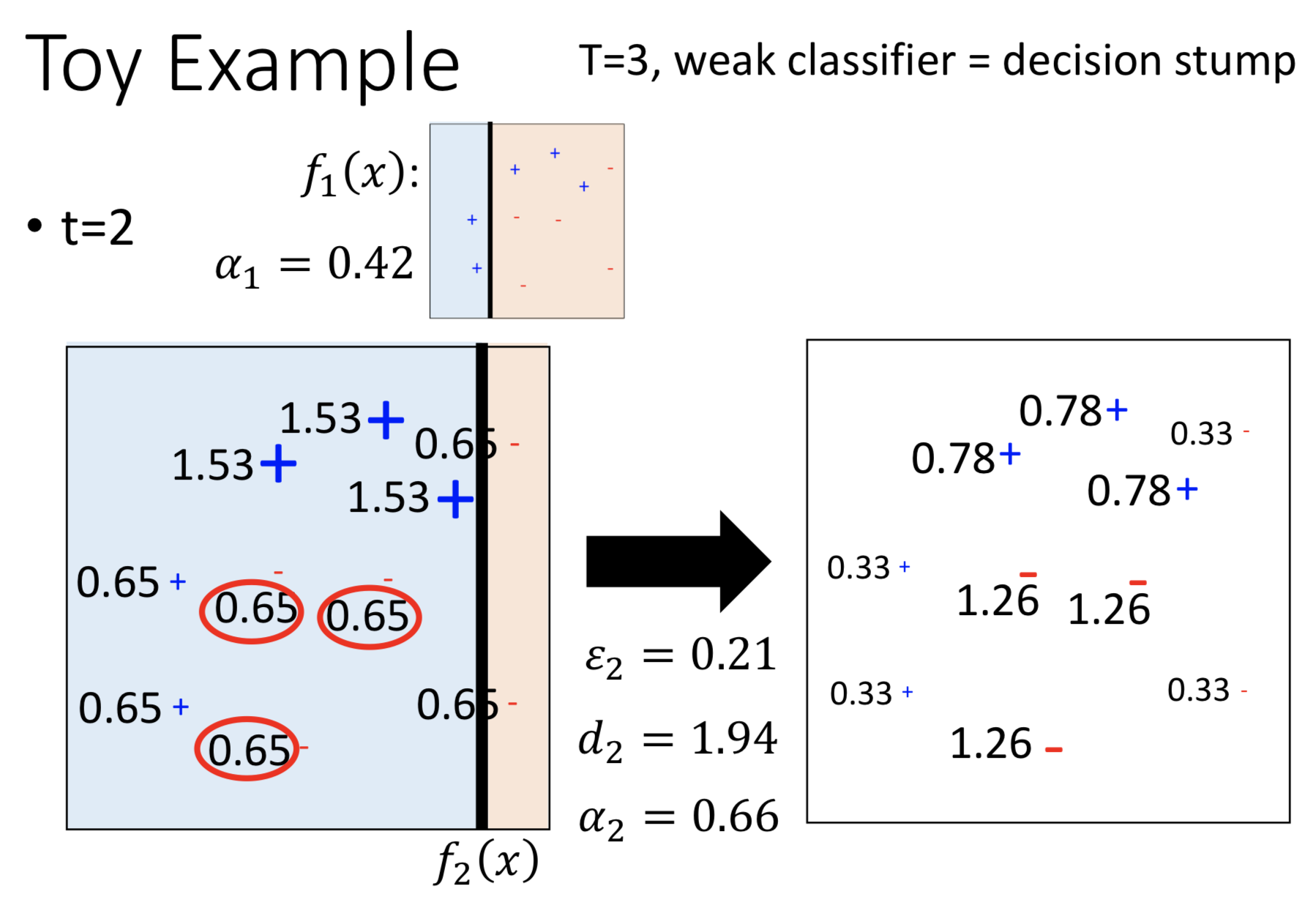
T=2,在$u_{2}$下学的一个分类器,同理计算出所有参数,得到$u_{3}$。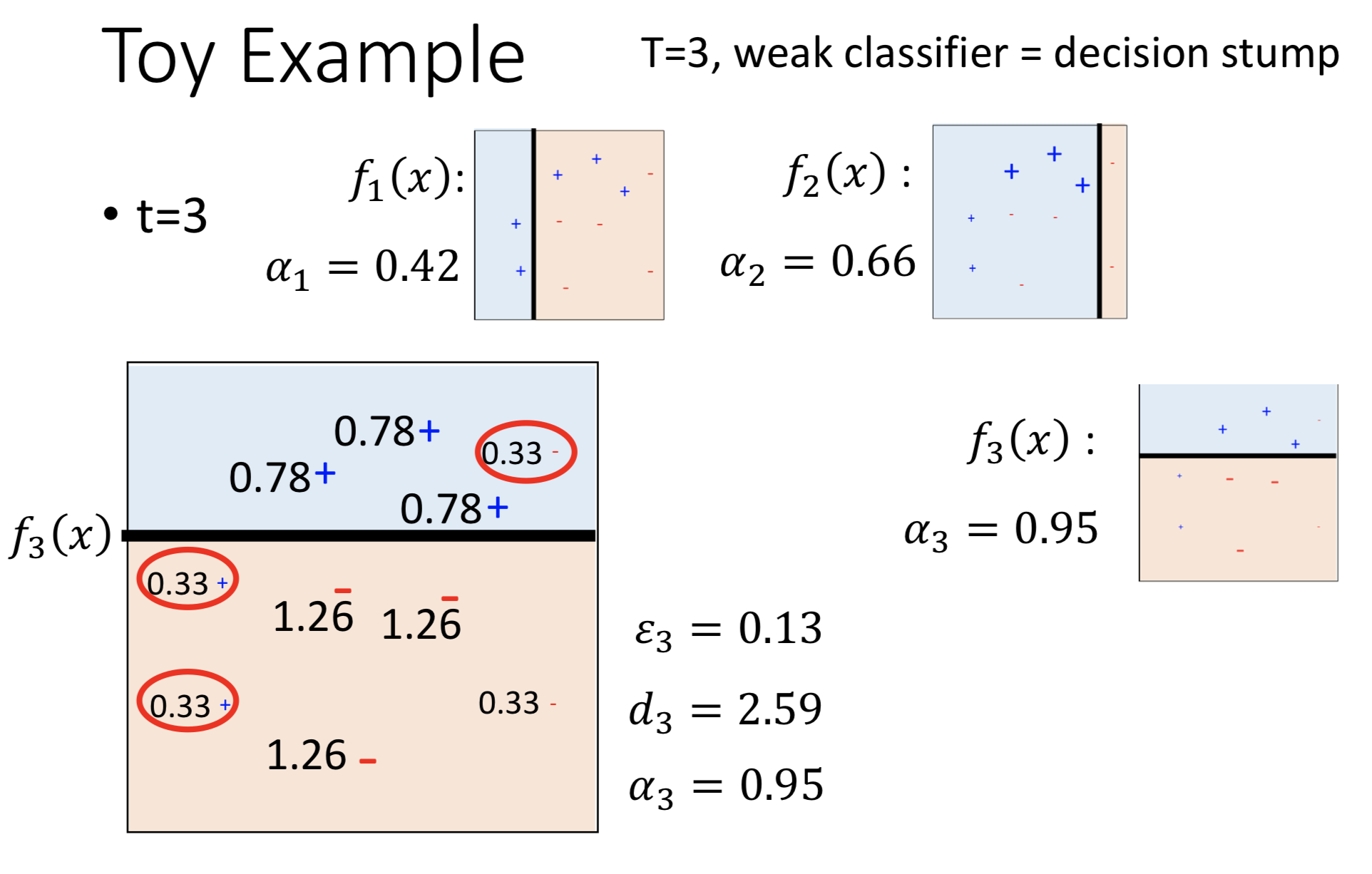
T=3,同上。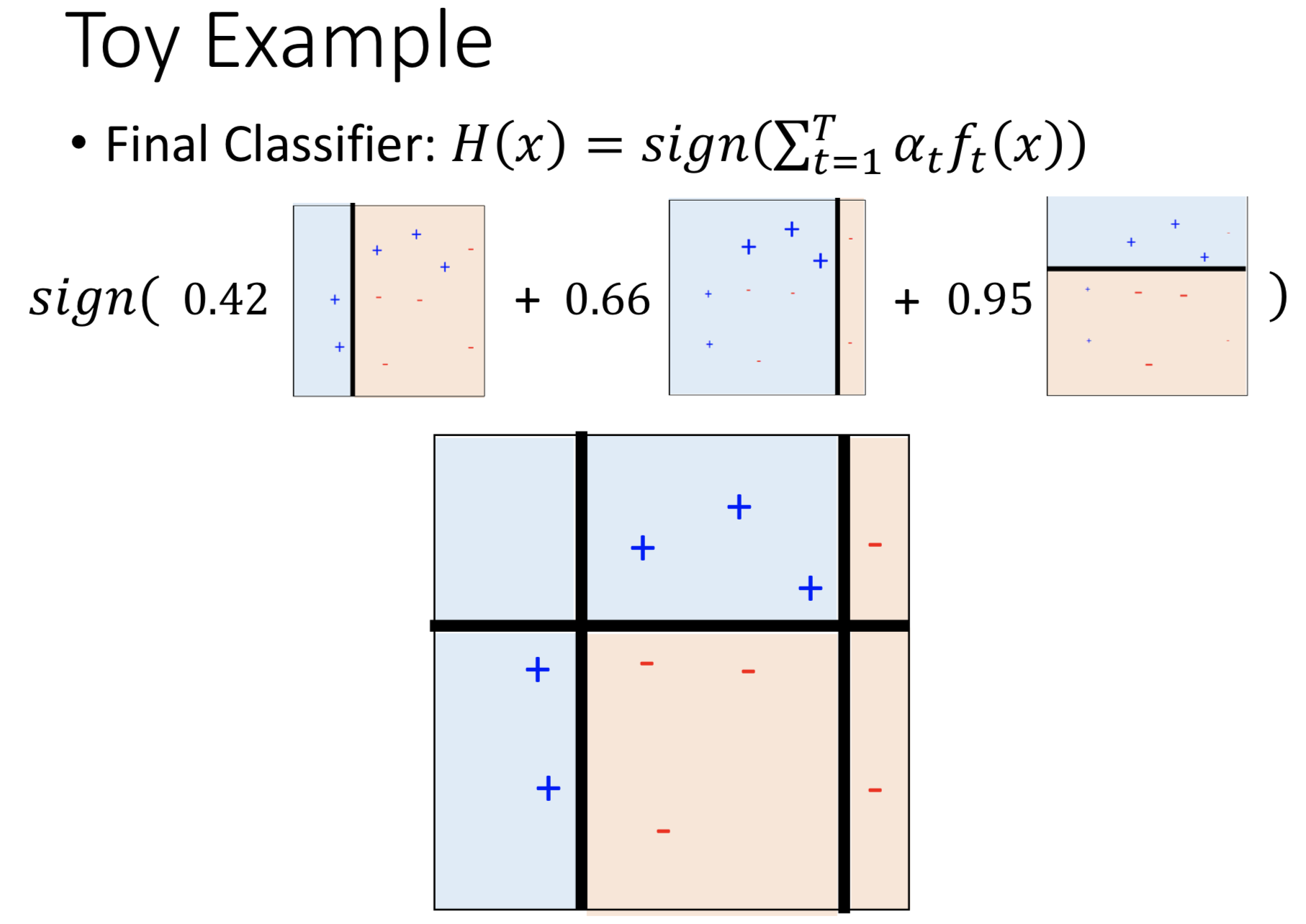
最后,把前面三个子模型加权累加,得到一个总的模型。
Boosting的一般形式

初始化一个函数$g_{0}(x)=0$(总模型)。假设我们要训练T个模型,每一步就是找到一个$f_{t}(x)$函数(子模型)和一个$\alpha_{t}$来提升上一个时刻的$g_{t-1}(x)$。(这里的直接就是每一个子模型都是对之前的所有的模型的进一步优化,即残差的优化)。
输出为最后T时刻的总模型$g_{T}(x)$(即所有子模型的累加),由于是二分类问题,再作符号判断得到总模型H(x)。
Gradient Boosting
GB是Boosting的一种实现方式。
假设我们定义Boosting的损失函数为L(g),我们可以理解为GB为一个整体模型,用梯度下降法优化。计算关于g(x)的偏微分,不断更新g(x),找得最优$g_{T}(x)$使得总模型有最优解。这里就是用梯度的思想来实现boosting的找一个$f_{t}(x)$函数(子模型)和一个$\alpha_{t}$来提升上一个时刻的$g_{t-1}(x)$。
当我们定义损失函数为上面的样子,代入GB公式里;这里要求上面两个红框里是至少要有同样的方向。
同方向的意义是指,在把两个式子看作向量的情况下,把两个作内积越大,两个式子越等价。从上面得到的式子可以看出,前半部分是权重u。我们发现,现在要找一个ft(x)来minimize error,会在每一笔data前乘以一个weight(maximizing希望同号的weight越大,$u_{t}$越大,在t-1时刻error 越大<—-这个没仔细看,还不确定)。且发现权重正好是我们在Adaboost里面的权重。(这里找出来的f就是Adaboost里面找得,就是说GB是更一般的形式,当把lossfunction定义为上式时,就等于Adaboost,也就是说Adaboost是在minimize这样的一个lossfun。GB可以替代其他的lossfun)
接下来的是$\alpha_{t}$。发现正好也是Adaboost里面的$\alpha_{t}$。