先看大佬是怎么说的:https://www.zhihu.com/question/21874816
以下是个人的简单理解,方便记忆。
特征分解是使用最广的矩阵分解之一,即我们矩阵分解成一组特征向量和特征值。
方阵 A 的特征向量(eigenvector)是指与A相乘后相当于对该向量进行缩放的非零向量v:
其中标量$\lambda$称为这个特征向量的特征值(eigenvalue)。
如果v是A的特征向量,那么任何缩放后的向量sv($s\in R$,$s≠0$)也是A的特征向量。此外,sv和v有相同的特征值。基于这个原因,通常我们只考虑单位特征向量。(单位向量$\parallel x\parallel _{2}=1$)
假设矩阵A有n个线性无关的特征向量{$v_1,v_2,…,v_n$},对应着特征值{$\lambda _{1},\lambda _{2},…,\lambda _{n}$}。我们将特征向量连接成一个矩阵,使得每一列是一个特征向量:$V = [v_1,v_2,…,v_n]$。类似的,我们也可以将特征值连接成一个向量$\lambda = [\lambda _{1},\lambda _{2},…,\lambda _{n}]^{T}$。因此A的特征分解可以记作:
不是每一个矩阵都可以分解成特征向量和特征值的。在某些情况下,特征分解存在,但是会涉及复数而非实数。在深度学习领域,我们通常只要分解一类有简单分解的矩阵。具体来讲,每个实对称矩阵都可以分解成实特征向量和特征值:
其中Q是A的特征向量组成的正交矩阵,$\Lambda$是对角矩阵。特征值$\Lambda _{i}$,i对应的特征向量是矩阵Q的第i列,记作$Q_{:,i}$。
一个简单的理解,如果把矩阵看作是运动,对于运动而言,最重要的当然就是运动的速度和方向,那么:
- 特征值就是运动的速度
- 特征向量就是运动的方向
既然运动最重要的两方面都被描述了,特征值,特征向量自然可以称为运动(即矩阵)的特征。反复运用矩阵乘法,矩阵所代表的运动最明显的特征,即速度最大的方向,就由最大特征值对应的特征向量展现了出来。
几何意义
说明下,因为线性变换总是在各种基之间变来变去,所以下面的画图都会把作图所用的基和原点画出来。
在$\vec{i}$,$\vec{j}$下面有个$\vec{v}$: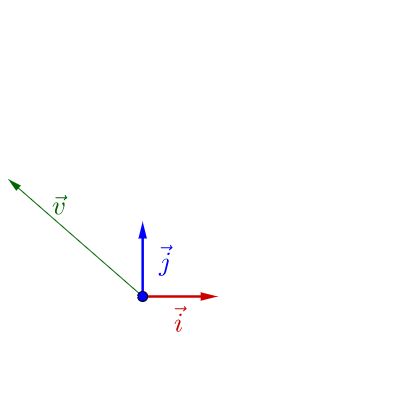
随便左乘一个矩阵A,图像看上去没有什么特殊的: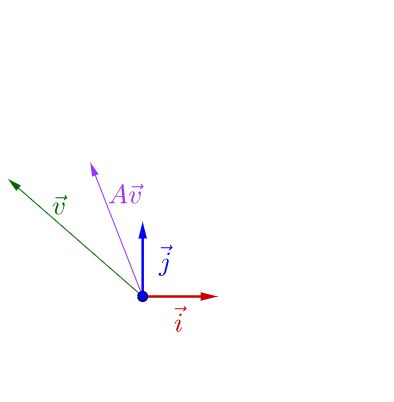
调整下$\vec{v}$的方向,图像看上去就有点特殊了: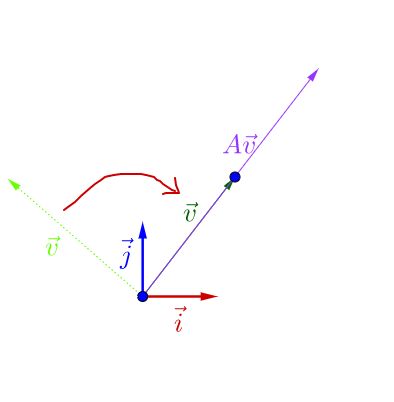
可以观察到,调整后的$\vec{v}$和$A\vec{v}$在同一直线上,只是$A\vec{v}$的长度相对$\vec{v}$的长度变长了。此时,我们就称$\vec{v}$是$A$的特征向量,而$A\vec{v}$的长度是$\vec{v}$的$\lambda$倍,$\lambda$就是特征值。从而,特征值与特征向量的定义式就是这样的: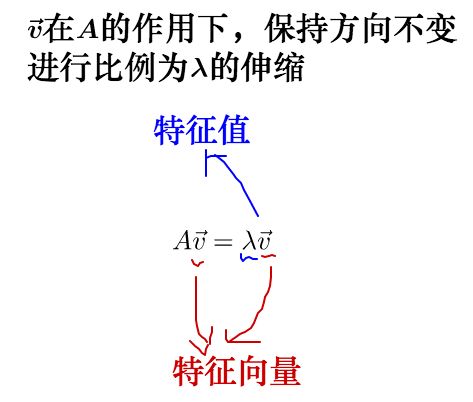
之前的$A$不止一个特征向量,还有一个特征向量: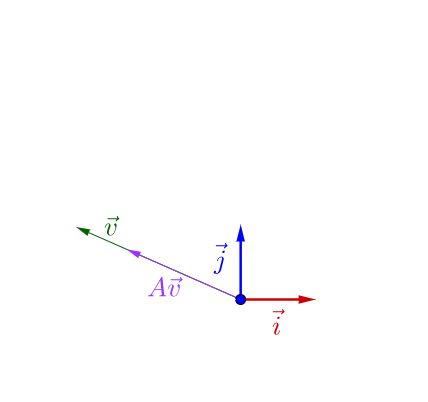
容易从$A\vec{v}$相对于$\vec{v}$是变长了还是缩短看出,这两个特征向量对应的特征值$\lambda$,一个大于1,一个小于1。
从特征向量和特征值的定义式还可以看出,特征向量所在直线上的向量都是特征向量: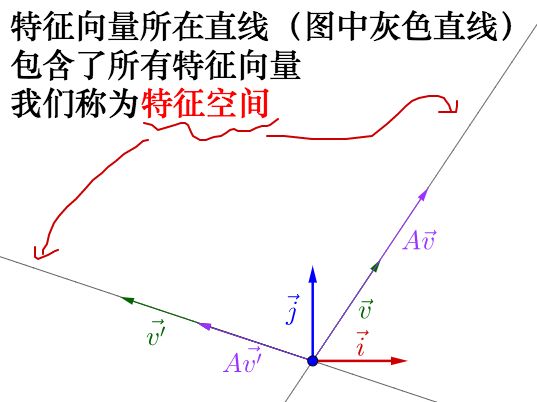
特征值越大,说明矩阵在对应的特征向量上的方差越大,功率越大,信息量越多。
例如图片压缩的例子,一副512*512的图片只保留前面50个的特征值(也就是最大的50个,其实也只占了所有特征值的百分之十),其它的都填0,就能复原出基本图像,效果还可以。其实一两百个特征值之和可能就占了所有特征值和的百分之九十了,其他的特征值都可以丢弃了。